Mecánica de Fluidos

Áreas Planas Sumergidas

En esta figura se muestra un tanque que tiene una ventana rectangular en una pared inclinada. Las dimensiones estándar y los símbolos utilizados en el procedimiento descrito más adelante se muestran en la figura y se definen de la siguiente manera:

F_R = Fuerza resultante sobre el área debida a la presión del fluido.

El centro de presión del área es el punto donde se considera que actúa la fuerza resultante.

El centroide del área es el punto en el que el área se balancearía si fuera suspendida en otras palabras el centro de masa o de gravedad de un cuerpo sólido.

S = Línea perpendicular a la línea de inclinación.

ʘ = Ángulo de inclinación del área.

h_c = Profundidad del fluido desde la superficie libre hasta el centroide del área.

h_p = Profundidad del fluido desde la superficie libre hasta el centro de presión.

L_c = Distancia desde el nivel de la superficie libre del fluido hasta el centroide del área, medida a lo largo del ángulo de inclinación del área.

L_p = Distancia desde el nivel de la superficie libre del fluido hasta el centro de presión del área, medida a lo largo del ángulo de inclinación del área.

B,H = Dimensiones del área de la figura.

Procedimiento para calcular la fuerza ejercida sobre un área plana sumergida

1.- Identificar el punto donde el ángulo de inclinación (ʘ) del área de interés interseca al nivel de la superficie libre del fluido. Esto puede requerir extender la superficie angulada o línea superficial del fluido. Este punto se llamará S.

2.- Localice el centroide del área a partir de su geometría.

(a continuación se presenta una tabla con los momentos de Inercia para figuras geométricas simples)

Figura	Diagrama	Momento de Inercia	Centroide
Rectángulo		Iz’ = b(h3)/12 Iy’ = b3(h)/12 Iz = b(h3)/3 Iy = b3(h)/3	Xg = b/2 Yg = h/2
Triángulo		Iz’ = b(h3)/36 Iz = b(h3)/12	Xg = b/3 Yg = h/3
Círculo		Iz = IY = (πr4)/4	G = R G = Radio
½ Círculo		Iz = Iy = (πr4)/8	Yg = 4R/3π Xg = R
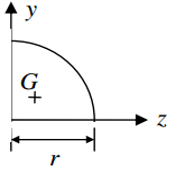
¼ de Círculo		Iz = IY = (πr4)/16	Yg = 4R/3π
Elipse		Iz = (π(a)b3)/4 Iz = (π(a3)b)/4	Yg = b Xg = a
Trapezoide		Ig = Z3(b2+4bB+B2)/36(b+B)	Yg=Z(b+2B)/3(b+B)

3.- Determina h_c como la distancia vertical desde el nivel de la superficie libre hasta el centroide del área.

4.- Determinar L_c como la distancia inclinada desde el nivel de la superficie libre hasta el centroide del área. Esta es la distancia de S hasta el centroide. Tenga en cuenta que h_c y L_c , se relacionan mediante: h_c = L_c senʘ.

5.- Calcule el área total A sobre la que se va a determinar la fuerza.

6.- Calcule la fuerza resultante a partir de:

F_R = γ (hc) A

γ = Peso Específico

7.- Calcule I_c , el momento de inercia del área alrededor de su eje centroidal.

8.- Calcule la ubicación del centro de presión a partir de:

L_p – L_c = I_c / L_c A

9.- Bosqueje la fuerza resultante que actúa en el centro de presión y es perpendicular al área.

10.- Muestre la dimensión L_p en un bosquejo en un dibujo. (Como en la imagen al inicio del documento)

11.- Dibuje las líneas de dimensión para L_c y L_p a partir de una línea de referencia trazada a través del punto S y perpendicular al ángulo de inclinación del área. (Como en la imagen al inicio del documento)

12.- Si desea calcular la profundidad vertical hasta el centro de presión h_p , se puede utilizar cualquiera de dos métodos.

Utilizando:

h_p = L_p Senʘ

O directamente a partir de:

h_p = h_c + [ (I_CSen²ʘ) / (h_c A) ]