Ejemplo de Empuje y Flotación

Ejemplo de Empuje y Flotación 1.- Un barco, con los costados verticales a la altura de la línea de flotación, pesa 4000 toneladas y en agua salada (γ = 1.025 kg/m3) tiene un calado de 6.6m. Al descargar 200 toneladas la profundidad de inmersión disminuye a 6.3m. ¿Cuál será el calado “d” del barco en agua dulce? (calado = Altura Sumergida) Como se desconoce la forma de la parte del barco sumergido en el agua, es preferible resolver el problema...

Read More

Fuerzas en una Superficie Curva Sumergida

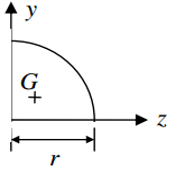
Distribución de la Fuerza Sobre una Superficie Curva Sumergida Para calcular la fuerza resultante sobre la superficie curva, debemos calcular los componentes de la fuerza (horizontal y vertical). Componente Horizontal La pared sólida vertical de la izquierda ejerce fuerzas horizontales sobre el fluido que está en contacto con ella en reacción de las fuerzas debidas a la presión del fluido. Esta parte del sistema se comporta de igual manera...

Read More

Flotabilidad y Empuje

Flotabilidad y Empuje La flotabilidad es la tendencia de un fluido a ejercer una fuerza de soporte sobre un cuerpo colocado en el fluido. La estabilidad se refiere a la capacidad que tiene un cuerpo, cuando está en un fluido, de regresar a su posición original después de ser inclinado con respecto a un eje horizontal. La fuerza de flotación actúa verticalmente hacia arriba a través del centroide del volumen desplazado. Fuerza de Flotación Fb...

Read More

Áreas Planas Sumergidas

Mecánica de Fluidos Áreas Planas Sumergidas En esta figura se muestra un tanque que tiene una ventana rectangular en una pared inclinada. Las dimensiones estándar y los símbolos utilizados en el procedimiento descrito más adelante se muestran en la figura y se definen de la siguiente manera: FR = Fuerza resultante sobre el área debida a la presión del fluido. El centro de presión del área es el punto donde se considera que actúa la fuerza...

Read More

Principios Básicos

Mecánica de Fluidos Conceptos Básicos Presión: La cantidad escalar que se obtiene al dividir la magnitud de una fuerza ejercida de forma perpendicular sobre alguna superficie entre el área de la misma. P = F/A P =  Presión sobre el área específica. (Pa = N/m = Pascal) F = Fuerza aplicada sobre el área específica. (N = Kg (m/s2) = Newton) A = Área sobre el cual es aplicada la fuerza. (m = Metros) Los fluidos se someten a grandes variaciones...

Read More